Silicon Oxidation Model

Deal and Grove’s model describes the kinematics of silicon oxidation. The model is generally valid for temperatures between 700 and 1300°C, partial pressures between 0.2 and 1 atmosphere, and for oxide thickness between 300 and 20,000°A for oxygen and water ambients.

Flux is the number of atoms or molecules crossing a unit area in unit time.

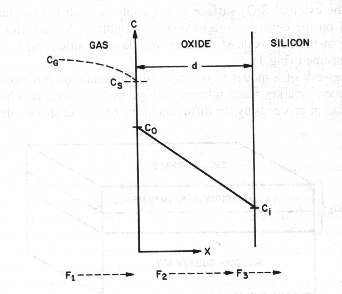
Fig. 2 Basic model for thermal oxidation of silicon [2]

Basic model for thermal oxidation of silicon [2]

The oxidizing species:

• Are transported from the bulk of the gas phase to the gas-oxide interface with flux F₁.

• Are transported across the existing oxide toward the silicon with flux F₂.

• React at Si-SiO₂ interface with the silicon with flux F₃.

Under steady state, all the fluxes are equal, F₁=F₂=F₃

• Assuming that the flux of the oxidant from the bulk of the gas phase to the gas-oxide interface is proportional to the difference between the oxidant concentration in the bulk of gas C_G and the oxidant concentration adjacent to the oxide surface C_S, we get

F₁=h_G(C_G-C_S) -----------------(1)

Where h_G is the gas phase mass-transfer coefficient. [1] [4]

• From Henry’s law, which states that the concentration of an adsorbed species at the surface of a solid is proportional to the partial pressure of that species in the gas just above the solid, we get

C₀=Hp_S and C^*=Hp_G

Where,

C₀ is the equilibrium concentration in the oxide at the outer surface.

C^* is the equilibrium bulk concentration in the oxide.

p_S is the partial pressure in the gas adjacent to the oxide surface.

p_G is partial pressure in the bulk of gas

H is Henry’s law constant.

• Using Henry’s law along with the ideal gas law we get,

C₀=Hp_S=HkTC_S where p_S=kTC_S and

C^*=Hp_G=HkTC_G where p_G=kTC_G

Substituting, C₀ and C^*, into equation (1), we get the following:

F₁=h(C^*-C₀) where h=h_G/HkT

• Oxidation is a non-equilibrium process with the driving force being the deviation of concentration from equilibrium. Henry’s law is valid only in the absence of dissociation effects at the gas-oxide interface. This implies that the species moving through the oxide are molecular.

• Flux of the oxidizing species across the oxide follows Fick’s law at any point d in the oxide layer.

F₂ = D(C₀-C_i)/d₀

Where

D is the diffusion coefficient

C_i is the oxidizing species concentration in the oxide adjacent to the oxide-silicon interface.

d₀ is the oxide thickness.

• Flux corresponding to the Si-SiO₂ interface reaction is proportional to the concentration of oxidizing species in the oxide adjacent to the oxide-silicon interface, C_i.

F₃=k_SC_i

Where k_S is the rate constant of chemical surface reaction for silicon oxidation.

• Under steady state conditions we have

F₁=F₂=F₃ and solving simultaneous equations we can find C_i and C₀.

• When diffusivity is very small C_i®0 and C₀®C^*. This is called diffusion-controlled case. It results from the flux of oxidant through the oxide (F₂) being small compared to the flux corresponding to the silicon-silicon dioxide interface reaction (F₃). Hence oxidation rate depends on the supply of oxidant to the interface and not on the reaction at the interface.

• When diffusivity is large, C_i=C₀. This is called reaction-controlled case, because an abundant supply of oxidant is provided at the silicon-silicon oxide interface and the oxidation rate is controlled by the reaction rate constant k_S and C_i.

• Combining various equations and assuming that an oxide may be present initially from a previous processing step, that is, d₀=d_i at t=0 the following equation can be generated. [2]

d₀² + A d₀ = B(t+t)

Where t represents a shift in the time axis to account for the presence of the initial oxide layer d_i.

Also,

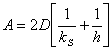
N₁ is the number of oxidant molecules incorporated into a unit volume of the oxide layer.