Mathematical Model for Ion Implantation

• As an ion enters the surface of the wafer it collides with atoms in the lattice and interacts with electrons in the crystal.

• Each nuclear or electronic interaction reduces the energy of the ion until it finally comes to rest within the target.

• Interaction with the crystal is a statistical process and the implanted profile can be approximated by the gaussian distribution function.

• The distribution is described mathematically by

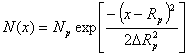
Where R_p is called projected range and is equal to the average distance an ion travels before it stops. The peak concentration N_p occurs at x=R_p. Because of the statistical nature of the process, some ions will be “lucky” and will go beyond the projected range R_p, and some will be “unlucky” and will fall short of R_p.

DR_p is the standard deviation or the spread of distribution about R_p. It is also called straggle.

DR_^, transverse straggle, defines the lateral motion of the ions and also has a gaussian profile.

The area under the impurity distribution curve is the implanted dose, Q, given by the following expression:

• An arbitrary distribution N(x) can be characterized in terms of its moments.

• The normalized first moment of an ion distribution is the projected range, R_p.

• The second, third and fourth moments are typically expressed in terms of three parameters: standard deviation (DR_p), skewness (g) and kurtosis(b).

• Skewness measures the asymmetry of the distribution: positive skewness places the peak of the distribution closer to the surface than R_p.

• Kurtosis measures the flatness of the top of a distribution.

• Note that Gaussian distributions have a skewness of 0 and a kurtosis of 3.[2] [1]

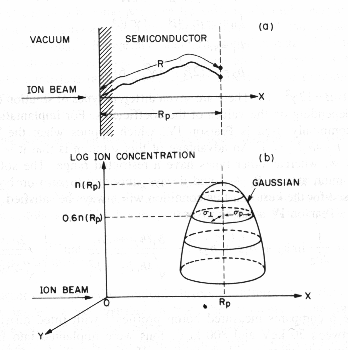
Fig. 3 Schematic views of the ion range (a) the total path length R is longer than the projected range R_p. (b) the stopped atom distribution is two-dimensional Gaussian.[2]