Constant-Source
Diffusion
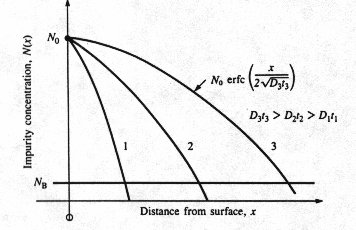
Fig 2 Constant-source diffusion results in a complementary
error function impurity distribution. The surface concentration N0 remains
constant and the diffusion moves deeper into the silicon wafer as the Dt
product increases. Dt can change as a result of increasing diffusion time,
increasing diffusion temperature, or a combination of both. [1]
A constant-source diffusion or constant surface
concentration or solid solubility limited predeposition / diffusion results in
a complementary error function
impurity distribution. The surface concentration N0 remains constant
and the diffusion moves deeper into the silicon wafer as Dt product increases.
Dt can change as a result of increasing diffusion time, increasing diffusion
temperature, or a combination of both.
Initial Condition:
At time t=0, impurity concentration at depth x and time t,
that is, N(x,t) is given by,
N (x, 0) = 0
Boundary Conditions:
At surface we have N(0,t) = N0 and N(¥,t) = 0 for x=¥
The solution of Fick's second law that
satisfies the initial and boundary conditions is given by
![]()
Where N0 is the surface concentration (atoms/cm2)
D is constant diffusivity in cm2/s
x is the distance in cm
t is the diffusion time in seconds
The table below gives some values of z= x/2(Dt)1/2
and erfc(z)
|
z |
erfc(z) |
|
0 |
1.0 |
|
0.5 |
0.5 |
|
1.0 |
1.7 |
|
1.5 |
0.35 |
|
2.0 |
0.005 |
|
2.5 |
0.0004 |
|
3.0 |
0.00002 |
|
¥ |
0 |