Models of
diffusion in solids
At
high temperatures point defects such as vacancies and self-interstitial atoms
are generated in a single-crystal solid. Diffusion in a solid can be visualized
as atomic movement of the diffusant in the crystal lattice by vacancies or
self-interstitials.
Diffusion by a vacancy
At
elevated temperature the lattice atoms vibrate around the equilibrium lattice
sites. Occasionally a host atom acquires sufficient energy to leave the lattice
site, becoming a self-interstitial atom
and creating a vacancy. When a
neighboring atom migrates to the vacancy site, it is called diffusion by a
vacancy. [2]
If
the migrating atom is a host atom, the diffusion is self-diffusion.
If
the migrating atom is an impurity atom, the diffusion is impurity diffusion.
Divalency
If
the impurity atom moves to a second vacancy that is at the nearest neighbor of
the original vacancy site, it is called diffusion assisted by a double vacancy or divacancy.
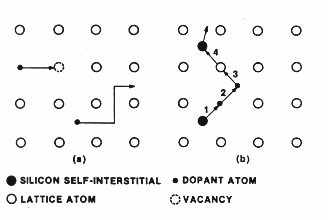
Fig.
1 Models of atomic mechanism for a two-dimensional lattice (a) Vacancy and
interstitial mechanism (b) Interstitialcy mechanism [2]
Interstitialcy mechanism
Interstitialcy
or the extended interstitial mechanism is shown in (b) above.
A
self-interstitial atom displaces an impurity (step 1) which in turn becomes an
interstitial atom (step 2). Subsequently the impurity atom displaces another
host atom (step 3) and the second host atom becomes a self-interstitial (step
4).
Smaller ionic radii impurities
diffuse faster through interstitial mechanism.
Atomic
diffusion mechanism in silicon
·
Dopant impurity atoms
occupying a substitutional site in silicon cannot move without the presence of
point defects.
·
The generation,
annihilation, and movement of point defects and their interactions with
impurity atoms affect the diffusion results and the measured diffusivities.
·
Diffusion in silicon
can be described by mechanisms involving impurity.
·
And point-defect
interactions, such as vacancies and interstitials, at different charge states.
Ionized Point Defects
Point
defects can become electrically active when they accept or lose electrons. A
vacancy can act as an acceptor by acquiring a negative charge V-.
V + e Û V-.
Similarly
a self-interstitial atom can act as an acceptor by acquiring a negative charge I-
I + e Û I-
Where
V represents a vacancy, I represents a Si self-interstitial.
A vacancy represents a lattice site
where the silicon atom is missing.
A self-interstitial is a silicon atom
that is not on a lattice site.[2]
Kickout Mechanism
If
an impurity atom occupying a substitutional site is "kicked out" by a
silicon self-interstitial atom, the impurity becomes an interstitial atom. It
could move to another vacancy site, kick out another lattice silicon atom some
distance away from the original lattice site or diffuse interstitially for some
distance.
As + ISi
Û AI
Where
As is an impurity atom occupying a lattice site.
ISi is the silicon self-interstitial
atom
AI is the impurity atom,
which is not occupying a lattice site.[6]
Dissociative Mechanism
If
an impurity atom occupying a substitutional site has left that site, and if it
becomes an interstitial atom and a vacancy is left behind, the reaction can be
described by the following equation, which is called the dissociative mechanism.
AS Û AI + V
If the impurity in AS
Û
AI + V is replaced by a
silicon atom, then it would describe the creation of a Frenkel pair, which is a vacancy and a self-interstitial pair. For
a perfect crystal at thermal equilibrium, the Frenkel pair implies that the
number of vacancies and interstitials are equal.
Intrinsic Diffusivity
When
the impurity concentration C(x), is
less than ni, the intrinsic carrier concentration, the diffusion
results can be described by a concentration independent diffusivity called intrinsic diffusivity Di
Extrinsic Diffusivity
When
the impurity concentration, including both substrate doping and the dopant
impurity, is greater than ni (T), intrinsic carrier concentration at
the diffusion temperature T, the silicon is considered extrinsic silicon and
diffusivity is considered as the extrinsic
diffusivity De.
Diffusivity
D can be expressed as follows:
D=D° + D-(n/ni) + D=(n/ni)2
+ D+(n/ni) + …
Where
D° represents the intrinsic diffusivity of impurity
interaction with a neutral point defect, D- represents the intrinsic
diffusivity of impurity interaction with a singly charged acceptor point
defect, D+ represents the intrinsic diffusivity of impurity
interaction with a singly charged donor point defect and D=
represents the intrinsic diffusivity of impurity interaction with a doubly
charged acceptor defects.
In
case of intrinsic silicon, C(x) << ni, so n=ni
Therefore
D»D° + D- + D= + D+ +
… and D depends on temperature alone from the relation D=D0exp (-EA/kT)
In
case of extrinsic silicon, C(x) >> ni, so n>>ni
and so D becomes a function of temperature and concentration of the dopant
impurity C(x).