Miller Indices

It is important to specify the orientation of crystal planes and directions because crystals may have different properties along different directions. A crystal plane is specified by its Miller Indices.

How to obtain Miller indices?

· Determine the intercepts of the plane on three Cartesian coordinates.

· Measure the distances of the intercepts from the origin in multiples of the lattice constant.

· Take the reciprocals of the intercepts and then multiply by the least common multiple of the intercepts.

Example: Find the Miller indices for the crystal planes shown in Fig. 4 (a) below. Assume the lattice constant is unity.

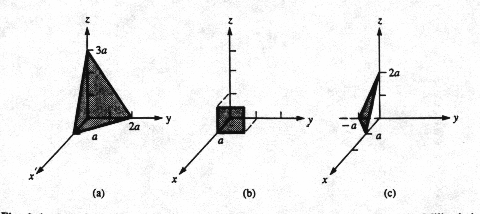
Fig. 4 Sample cubic crystal planes [1]

In the figure above the plane intercepts the three crystal axes at (1,0,0), (0,2,0) and (0,0,3) or simply (1,2,3). The reciprocals are 1/1, 1/2,1/3.

Multiplying by 6, these fractions are reduced to 6,3,2 that are the Miller Indices. The plane is known as the (6 3 2) plane.

Exercise: Find the Miller indices for the crystal planes in Fig. 4 (b) and (c).

· Note that the direction of a crystal plane is normal to the plane itself and is designated by brackets of the same Miller Indices. For example the direction of the (111) plane is written as [111].

· Using braces can show families of equivalent planes. The notation {100} refers to the six planes on the cube faces.

· Using angle brackets can show families of equivalent vectors. The notation <100> refers to the six directions ±x, ± and ±z.